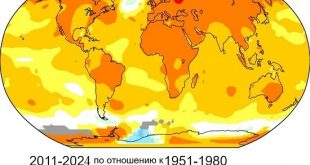
Термин фрактал (от латинского fractus, означающего “сломанный”) был введен математиком Бенуа Мандельбротом в 1975 году. В своей основной работе «Фрактальная геометрия природы“ он определяет стохастические фракталы (случайные) как «грубую или фрагментированную геометрическую форму, которую можно разделить на части, каждая из которых является (по крайней мере, ориентировочно) уменьшенной копией целого”.
Если совсем просто, то стохастические фракталы — линии и поверхности случайной формы.
Для нас людей, кодеров природы, мы должны задать себе вопрос: можем ли мы описать наш мир с помощью евклидовой геометрии? Очевидно нет!
Известно, что Евклидова геометрия (в честь древнегреческого математика) опирается на понятия точки, прямой, плоскости. Но как описать с точки зрения математики деревья, которые стоят на улице, листья, которые свисают с этих деревьев, молнии от вчерашней грозы, цветную капусту, которую ели на ужин, кровеносные сосуды в организме, горы и береговые линии, которые покрывают землю многих стран? Большинство вещей в природе не могут быть описаны идеализированными геометрическими формами Евклидовой геометрии.
Большинство вещей в природе не могут быть описаны идеализированными геометрическими формами Евклидовой геометрии.
Поэтому, если мы хотим начать строить вычислительные проекты с шаблонами за пределами эллипса простых форм пришло время нам узнать о концепциях и методах моделирования мира из серии книг «Фракталы и Хаос».
Фракталы повсюду?
Очень часто примером фрактальной кривой является береговая линия любой страны. Глядя на эту очень необычную линию в крупном масштабе — это действительно очень похоже на то, что можно наблюдать, глядя точнее на небольшую часть морского берега. В известных и предлагаемых книгах утверждается, что стохастические фракталы везде.
Фрактал имеет похожую форму как и его отдельная часть.
Собственно, в последнее время физики и математики с использованием модели фрактала представляли собой активную научную область с множеством приложений: инфографика, геофизика, явления турбулентности, спутниковые снимки, моделирование текстур, классификация и сегментации, сжатие, водяные знаки, где эти понятия потенциально интересны.
Фракталы соответствуют общей идее, которую можно легко понять с интуитивной точки зрения, что данный объект, особенно текстурированная область, может быть представлен по схожим характеристикам и «повторяется» при разных масштабах. Эту разностороннюю идею, однако, можно перевести в различные формы с математической точки зрения.
Стохастические фракталы всегда будут фокусироваться на более или менее сложных моделях для описания текстур чего либо. Как показано в литературе, эти модели опираются на понятие статистической «самоподобности». Эта концепция лежит в основе соответствующих моделей для нескольких природных явлений. В то же время нестационарная структура самоподобных процессов лежит в основе самых последних обработок изображений и сигналов.
Фрактальные множества теперь являются ключевым компонентом большей части математики, начиная от динамических систем, групп преобразований, стохастических процессов и заканчивая современным анализом. Уже давно известно, что теории фракталов и математические вероятности связаны.
Хотя самоподобие является ключевой чертой фракталов, важно понимать, что самоподобие само по себе не делает фрактал. В конце концов, линия самоподобна. Линия выглядит одинаково в любом масштабе и может рассматриваться как состоящая из множества маленьких линий.
Фракталы характеризуются тонкой структурой в малых масштабах (продолжайте увеличивать график фондового рынка, и вы будете продолжать находить колебания) и не может быть описано Евклидовой геометрией. Если вы можете сказать: “это линия!” тогда это не фрактал.
В настоящее время существует теоретическая база, описывающая динамику экономических процессов, прогнозирование катаклизмов, диагностики заболеваний.