Булева логика служит основой анализа обоснованности логических суждений, так как она охватывает многозначный характер заявлений, которые могут появиться. Суждения могут быть либо истинные, либо ложные. Этот метод из двух логических элементов имеет многозначный характер.
Эти бинарные операции используются сейчас в электронных вычислительных машинах при их проектировании и эксплуатации.

Открыл Булеву логику британский математик Джордж Буль. Эта логическая теория выступает как основа современных цифровых компьютеров и других электронных устройств. С этой точки зрения британский математик считается одним из основателей математической логики, который начал математический анализ мысли и исследования законов мысли. Он представил общий символический метод логического вывода на основе ‘закона мышления’, опубликованный в 1854 году.
Булева логика изучает логические операции над высказываниями. Высказывания могут быть истинными и ложными. Математика признали отцом современных информационных технологий и осознали что его идея была революционной.
Булева логика представляется собой самый простой из всех существующих и является основой вычислительной техники.
Компьютеры и логика неразделимые
Первые компьютеры были задуманы как автоматические арифметические системы и, хотя их создатели были в курсе, что закономерность должна что-то делать со всем этим, они не были на 100% уверены в том, как и почему.
С работ Буля началась современные рассуждения разъединившие пути с “законами мышления”. В том-то и дело, что сегодня у нас нет четкого представления, какие законы управляют мыслью. Если бы человек выяснил как управлять мыслью искусственный интеллект был бы закрыт.
Булева логика очень легко объясняется и понимается:
- некоторые высказывания Р являются либо истинными, либо ложными, не может быть что-нибудь между ними (это называется закон исключения третьего);
- сформулированы другие высказывания, которые являются истинными или ложными, путем сочетания этих исходных утверждений вместе с использованием основных операторов и, или и не.
Например, если Р истинно, то Р не ложно так, если “сегодня понедельник” истинно, то следующий день (сегодня понедельник) является ложным. Мы часто переводим логическое выражение на русский язык “сегодня не понедельник”, и это легче осознать, что это ложь, если сегодня действительно понедельник.
Основные логические операции
Основные логические операции по Булю рассматриваемые со стороны их значений (истина или ложь)
Логическое умножение (конъюнкция) — И
Логическое сложение (дизъюнкция) — ИЛИ
В 1854 году Буль опубликовал расследование законов мышления, на которых основал математические теории логики и вероятностей. Британский математик подошел по новому сводя простую алгебру логики, включающую математику. Он указал на аналогии между алгебраическими символами и тем, что представляют собой логические формы. Он начал с алгебры логики называемой сейчас Булевой алгеброй, которая в настоящее время находит применение в программировании во всех областях деятельности человека.
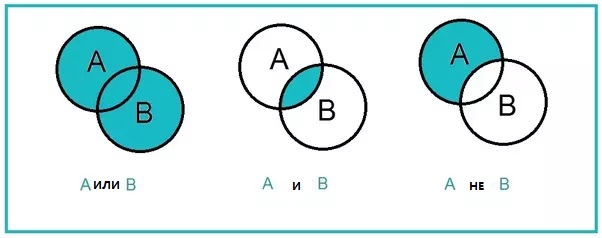



Умножение И