Величайший математик Евклид (III век до н. э.) развил математическую аксиоматику, подчеркнув наиболее важные поворотные моменты в основах пространственных структур и их отношений. Целых тринадцать томов древнегреческого математика Евклида посвящены различным разделам геометрии.
Элементы математика Евклида составляют одно из самых влиятельных научных произведений в истории человечества. Суть заключается в логическом развитии геометрии и других разделов математики.
Элементы Евклида изучаются по времени уже 24 века на многих языках, начиная, конечно, с греческого оригинала, затем на арабском, латыни и многих современных.
Основная идея математика Евклида
Основная идея математика Евклида состоит сначала определенных аксиом, которые считаются истинными, а затем — без какого-либо дальнейшего “ввода извне” — использование чисто дедуктивных методов для установления набора теорем.
Евклид фактически привел 10 аксиом (5 «постулатов “и 5” общих понятий“).
Постулаты и аксиомы – научные понятия принимаемые без доказательства.
Постулаты:
- можно провести прямую линию из любой точки в любую другую точку;
- отрезом прямой можно продолжить неограниченно;
- можно описать круг с любым центром;
- все прямые углы равны друг другу;
- постулат параллельности — параллельные линии никогда не встречаются (может показаться очевидным, но на самом деле оказывается неверным для физического искривленного пространства в нашей Вселенной.)
Общие понятия:
- вещи, которые равны одной и той же вещи, также равны друг другу;
- целое больше части;
- совмещающиеся друг с другом равны между собой;
- равные добавляются к равным, целые равны;
- равные вычитаются из равных, остатки равны.
На основе своих аксиом математик Евклид затем сформулировал 465 теорем.
Многие из них были о 2D и 3D геометрии; некоторые были об арифметике и числах. Среди них было много известных результатов, таких как теорема Пифагора, неравенство треугольника, тот факт, что существует пять Платоновых тел, иррациональность и тот факт, что существует бесконечное число простых чисел. Но, конечно, не все из них знамениты, а некоторые кажутся нам сейчас довольно малоизвестными. Евклид никогда не дает никакого объяснения о том, почему он выбирает теоремы, которые он решает из всех бесконечно многих возможностей. Понимание и объяснение вытекает само собой.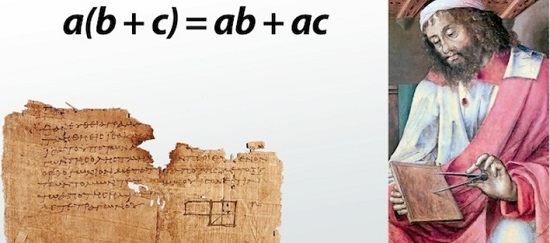
У нас нет никаких оригинальных решений сейчас, но существуют версии, написанные несколькими столетиями позже. Они написаны по-гречески, и каждая теорема объясняется словами, обычно со ссылкой на алгоритмы решения. У Евклида были в основном современные алгоритмы, и он даже обозначал точки и углы греческими буквами — несмотря на то, что идея переменных, обозначающих числа, не была изобретена до конца 1500-х годов.
Существует стилизованный способ с помощью которого математик Евклид сформулировал свои теоремы.
И насколько мы можем судить в первоначальной версии все, что было сделано, — это формулировка теорем. Не было никакого объяснения, почему теорема может быть истинной и никаких доказательств не предлагалось. Но прошло совсем немного времени, прежде чем люди начали заполнять доказательства, и вскоре появился стандартный набор доказательств, в котором каждая конкретная теорема была построена из других и, в конечном счете, из аксиом.
Было напечатано более тысячи изданий математика Евклида (вероятно, больше, чем любая другая книга, кроме Библии), и чтение его книг до недавнего времени было частью любого серьезного образования.
Вычислительный Евклид
- Основные статистические данные:
Как известно, элементы математика Евклида представляли на протяжении веков саму модель научного и дедуктивного рассуждения, а их распространение и влияние в Европе были только в соответствии с Библией и несколькими другими писаниями церкви. Они переводились, редактировались и комментировались сотни раз, и эти издания и комментарии формировали научный инструментарий, методологические стандарты и математический язык многих веков.
Теоремы Евклида использовались для построения дальнейших и более смелых математических теорий или применялись в физических науках, в то время как структура доказательств изучалась математиками, логиками и эпистемологи как идеал самого разума. В этой связи особую историческую роль сыграли принципы, служившие основанием и фундаментом всего строительства.
Математик Евклид начал формулировать свои элементы с нескольких недоказанных предположений для того, чтобы установить великую математическую систему. Однако в античности система принципов Евклида неоднократно обсуждалась и оспаривалась: были найдены некоторые пробелы в доказательствах и недостающие аргументы, снабженные дополнительными аксиомами. Некоторые принципы были доказаны с помощью более простых способов или изменены, чтобы удовлетворить философские сомнения или удовлетворить архитектурные соображения. Еще несколько были добавлены, чтобы расширить геометрические результаты за пределы границ, установленных Евклидом. Эти изменения в системе принципов, лежащих в основе элементарной математики, были одними из наиболее важных результатов фундаментальных исследований, проведенных в позднем Средневековье XIV—XV вв.
Развитие элементов великого математика Евклида
От Средневековья до начала девятнадцатого века сотни различных изданий элементов давали свои собственные принципы для одного и того же раздела математических теорем. 
В то время как утверждения евклидовых положений оставались более или менее одинаковыми, а сами доказательства редко менялись, мы наблюдаем в этот период замечательный взрыв новых принципов, направленных на строгость, систематизацию и улучшение работы Евклида. Об огромном творческом потенциале этих фундаментальных попыток свидетельствует открытие около 350 различных аксиом для элементарной математики, причем в некоторых работах используется до пятидесяти обоснований теорем элементов (сам Евклид, вероятно, имел только с десяток решений).
Многие из этих новых аксиом имеют большое математическое значение и ввели в основу математики несколько важных идей, которые получили полное развитие только в XIX и XX веках. Они касаются вопросов непрерывности в евклидовой плоскости, свойств падения в двух или трех измерениях, отношение эквивалентности на множестве геометрических фигур и движения, параллельного постулата и Евклидовой метрики или первых попыток аксиоматизации арифметики, алгебры, логики и математики. Наиболее известные работы на основе математики повлияли на современные формальные исследования аксиоматики.
